Unveiling The Power Of Self-Organizing Maps In Python: A Comprehensive Guide

Unveiling the Power of Self-Organizing Maps in Python: A Comprehensive Guide

Related Articles: Unveiling the Power of Self-Organizing Maps in Python: A Comprehensive Guide

Introduction

With great pleasure, we will explore the intriguing topic related to Unveiling the Power of Self-Organizing Maps in Python: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Self-Organizing Maps in Python: A Comprehensive Guide

The field of machine learning is constantly evolving, offering new and powerful tools to analyze data and extract meaningful insights. Among these tools, the Self-Organizing Map (SOM), also known as a Kohonen map, stands out as a versatile and intuitive technique for data visualization and dimensionality reduction. This article delves into the intricacies of SOMs, exploring their implementation in Python, their diverse applications, and the advantages they bring to data analysis.

Understanding the Essence of Self-Organizing Maps

At its core, a Self-Organizing Map is an unsupervised learning algorithm that transforms high-dimensional data into a low-dimensional representation, typically a two-dimensional grid. This grid, often referred to as the "map," serves as a visual representation of the data’s underlying structure, revealing patterns and relationships that might be obscured in the original high-dimensional space.

The fundamental principle behind SOMs is competitive learning. The algorithm iteratively adjusts the weights associated with each node in the map, striving to create a topology-preserving mapping of the input data. This means that nodes representing similar data points are positioned closer together on the map, while dissimilar points are placed further apart.

The Mechanics of SOM Training

The training process of a SOM involves the following steps:

1. Initialization: The map is initialized with random weights for each node.
2. Input Presentation: A data point is randomly selected from the input dataset.
3. Winner Determination: The algorithm identifies the node in the map whose weight vector is closest to the input data point. This node is declared the "winner."
4. Neighborhood Update: The weights of the winning node and its neighbors are updated to become more similar to the input data point. The strength of the update decreases with distance from the winning node, creating a neighborhood effect.
5. Iteration: The process of input presentation, winner determination, and neighborhood update is repeated for a large number of data points, allowing the map to gradually adapt to the underlying structure of the data.

Python Implementation: A Practical Approach

Python, with its rich ecosystem of libraries, provides a convenient platform for implementing SOMs. The minisom library, specifically designed for SOMs, offers a user-friendly interface and efficient algorithms.

Code Example: Visualizing Fashion MNIST Dataset

from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml

# Load Fashion MNIST dataset
X, y = fetch_openml('Fashion-MNIST', version=1, return_X_y=True, as_frame=False)

# Normalize data
X = X / 255

# Create SOM with 10x10 grid
som = MiniSom(10, 10, X.shape[1], sigma=1.0, learning_rate=0.5)

# Train SOM
som.train_batch(X, 1000)

# Visualize the map
plt.figure(figsize=(10, 10))
plt.pcolor(som.distance_map(), cmap='viridis')
plt.colorbar()
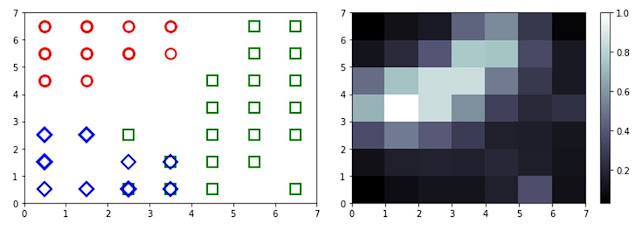
plt.show()

This code snippet demonstrates the basic steps of creating and training a SOM in Python. It loads the Fashion MNIST dataset, normalizes the data, creates a 10×10 map, trains the map, and finally visualizes the distance map, which reveals the spatial organization of the data on the map.

Benefits of Using Self-Organizing Maps

The application of SOMs brings several advantages to data analysis:

• Dimensionality Reduction: SOMs effectively reduce the dimensionality of high-dimensional data while preserving the underlying relationships between data points. This allows for visualization and analysis of complex datasets in a more comprehensible manner.
• Data Visualization: The two-dimensional map provides a visual representation of the data’s structure, revealing clusters, outliers, and patterns that might be difficult to discern in the original high-dimensional space.
• Feature Extraction: SOMs can be used to identify relevant features in the data. The weights associated with each node represent the feature values that are most prominent in the corresponding region of the data space.
• Anomaly Detection: Outliers in the data tend to be mapped to isolated regions on the SOM, making them easy to identify.
• Data Clustering: SOMs can be used for unsupervised clustering, grouping similar data points together based on their proximity on the map.

Applications of Self-Organizing Maps

The versatility of SOMs makes them applicable to a wide range of domains:

• Image Analysis: SOMs can be used for image segmentation, feature extraction, and image compression.
• Speech Recognition: SOMs can be used to analyze speech patterns and identify different speakers.
• Medical Diagnosis: SOMs can be used to analyze medical data and identify potential diseases or abnormalities.
• Financial Analysis: SOMs can be used to identify patterns in financial data, such as market trends or customer behavior.
• Marketing and Customer Segmentation: SOMs can be used to segment customers into groups with similar characteristics, allowing for targeted marketing campaigns.

Frequently Asked Questions (FAQs) About Self-Organizing Maps

Q: What are the hyperparameters of a SOM, and how do they affect the model’s performance?

A: The primary hyperparameters of a SOM are:

• Map Size: The number of nodes in the map, typically a two-dimensional grid. Larger maps can capture more complex structures but require longer training times.
• Neighborhood Function: Determines the shape and size of the neighborhood around the winning node. The most common functions are Gaussian and bubble.
• Learning Rate: Controls the rate at which the weights are updated. A higher learning rate leads to faster convergence but can also lead to instability.
• Sigma: Determines the spread of the neighborhood function. A larger sigma results in a wider neighborhood, influencing a larger area of the map during weight updates.

Q: How do I choose the optimal map size for my data?

A: The optimal map size depends on the complexity of the data and the desired level of detail. Start with a relatively small map and gradually increase the size until the map captures the desired level of structure. Experimentation and visualization of the map can help determine the optimal size.

Q: What are the limitations of SOMs?

A: While powerful, SOMs have some limitations:

• Sensitivity to Initialization: The initial weights of the map can influence the final outcome.
• Computational Complexity: Training a SOM can be computationally expensive, especially for large datasets.
• Interpretation Challenges: Interpreting the structure of the map can be subjective and requires careful consideration of the context.

Tips for Effective Use of Self-Organizing Maps

• Data Preprocessing: Standardize or normalize the data before training the SOM to ensure that all features contribute equally to the map.
• Hyperparameter Tuning: Experiment with different hyperparameter values to optimize the performance of the model.
• Visualization: Use visualizations to understand the structure of the map and identify patterns in the data.
• Validation: Evaluate the performance of the SOM using appropriate metrics, such as the quantization error or the topographic error.

Conclusion

Self-Organizing Maps offer a powerful and intuitive approach to data analysis, providing valuable insights into complex datasets. Their ability to reduce dimensionality, visualize patterns, and extract features makes them a valuable tool in various domains. By understanding the principles behind SOMs and leveraging the capabilities of Python libraries like minisom, data scientists can unlock the potential of this versatile technique to gain deeper understanding and extract meaningful insights from their data.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Self-Organizing Maps in Python: A Comprehensive Guide. We hope you find this article informative and beneficial. See you in our next article!